High Precision Electromagnetic Micro Current Sensor Used to Measure Leakage Current
WANG Wen，QIAO Ji-ping，LIN Ling-yan，SONG Jian-cheng
( Taiyuan University of Technology，Coal Mine Electrical Equipment and Intelligent Control Key Laboratory，Taiyuan 030024，China)
Abstract: It's difficult for ordinary small current sensor to meet the requirements of measuring micro current． A high preci- sion electromagnetic micro current sensor for on-line monitoring of leakage current was developed． Anti-jamming was measured by weak signal conditioning circuit enhancement． By designing signal conditioning circuit and writing program of error measurement in the LabVIEW，it turns out that the measuring limit has reached 20 μA，the precision of is up to 0． 5% ，which improved the res- olution and accuracy effectively． The experimental results show that the current sensor can measure microamps level of leakage current． Keywords: micro current sensor; conditioning circuit; LabVIEW; amplitude error; phase error
通过在线监测技术可以获得高压电机、电力电缆、避雷器等电气设备的绝缘状态，而在线监测的关键技术是泄漏电流的测量。由于泄漏电流的数量级均在几 μA 到几十 μA，普通的小电流传感器难以满足需求。因此，研制一种高精度的微电流传感器对电气设备绝缘状态的在线监测具有重要意义。
对于微电流传感器的研究始于 20 世纪 50 年代， 之后很多学者在提高灵敏度和带宽方面对微电流传 感器进行了改进。2008 年，华中科技大学采用整合两个罗氏线圈的方法提高了微电流传感器的灵敏度，实 现了高频脉冲信号的可靠检测。2010 年，重庆大学研制的无源微电流传感器，综合应用软硬件抗干扰以及 锁相倍频跟踪技术，解决了有源电流传感器存在零漂的技术难题，检测范围为 0． 1 mA ～ 1 A。目前研制出的微电流传感器虽然精度及灵敏度有了很大的提高， 但是仍旧无法准确测量几十 μA 的泄漏电流。
针对上述问题，从单匝穿心式电流传感器原理入
手，并对输出的微弱信号进行处理，利用频谱分析法测量传感器的误差。
1 电流传感器结构设计
1． 1 电流传感器测量原理
电流传感器采用环形铁芯，结构如图 1 所示。
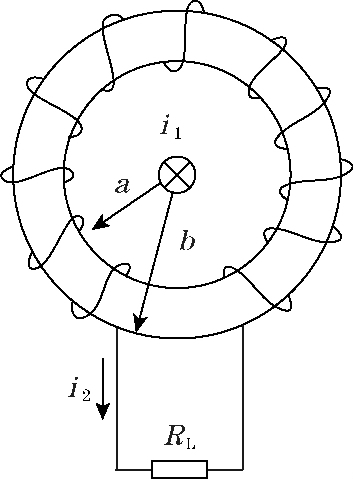
图1 电流传感器结构
一次线圈 N1 为一匝，二次匝数 N2 较多。一次线圈通过正弦交流电流 I 时［1］，二次感应电压产生输出电流 I2 ，通过磁感应作用相互耦合。理想情况下可以得到:
I1 N1 = I2 N2 ( 1)
1. 2 电流传感器误差因素分析及结构设计
电流互感器的误差是反转 180° 的二次电流相量
按照额定电流比折算至一次侧后，与实际一次电流相量之差，对实际一次电流相量的比值［2］，表示为
－ K I
－ I
－ N I
一种软磁材料，初始磁导率 μ
为 8 × 104 ，最大磁导率
ε = ln 2 1 × 100% = 2 0 × 100% ( 2) 0
式中 K1n
I1 1 1
= N2 为变比。
N
高达 6 × 105 ，具有低损耗、低矫顽力等优点［4］，适合用作电流传感器的磁芯。
1
考虑激磁电流的影响时:
I1 N1 + I2 N2 = I0 N1 = Hl ( 3)
式中 I0 为激磁电流。
从式( 2) 中可知，误差为激磁安匝与一次安匝相量之比的百分数。将二次侧折算至一次侧后的等效电路［3］如图 2 所示。
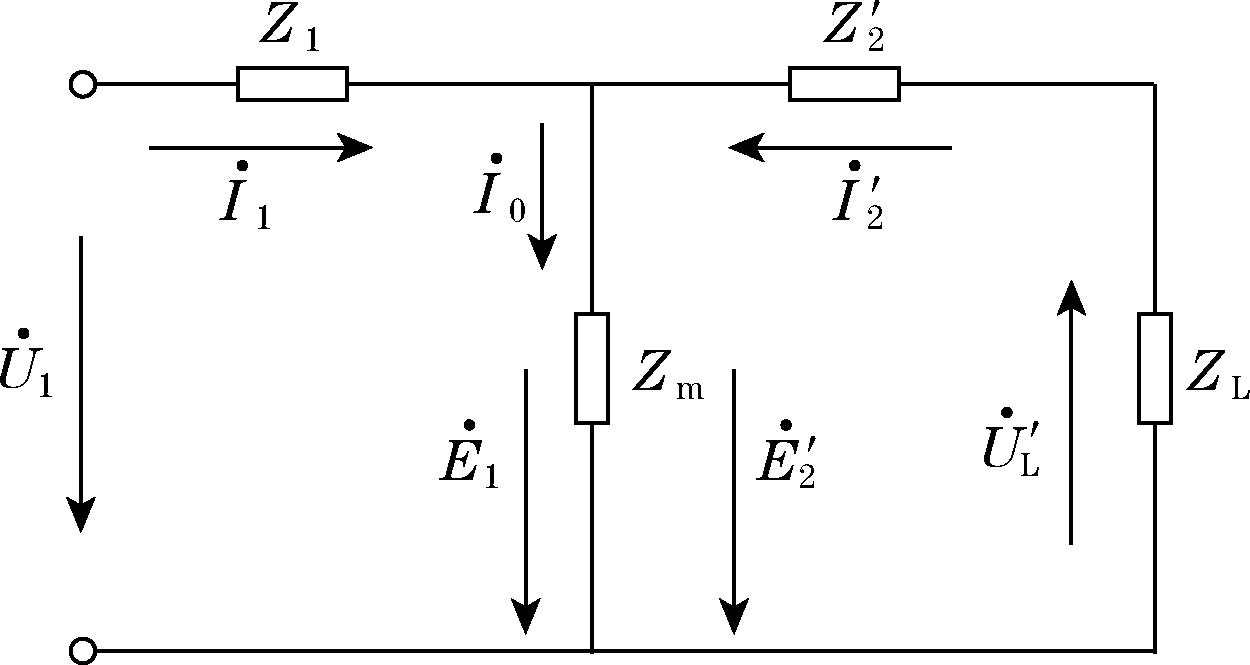
图 2 等效电路图
则误差公式可表示为
电流传感器结构的设计包括: 平均磁路长度的设
计及内外径的设计。当这些参数固定后，磁路长度和 截面积均可求出。根据式( 8) 得，铁芯的磁路 l 越小，
截面积 S 越大，误差就越小。当铁芯尺寸越小，测量
性能越好。但由于电流传感器穿心式的结构，需考虑所测导线的粗细。一般磁芯的高度满足 1. 5 ( D － d)
≤h≤2( D － d) 。最终确定铁芯尺寸内径 d = 25 mm，
外径 D = 40 mm，厚度 h = 25 mm。在对二次侧匝数和
负载进行选择时，本文根据图3 搭建实验测量平台，利用高精度数字万用表观察输出电压变化［5］，分别绕制 100，200，400 匝进行实验，当匝数为 200 匝时，测量数
据最稳定。因为在内径一定的情况下需保证匝数均匀分布，所以最终选择 229 匝。根据式( 8) 得出，Z 越
小，误差越小。但是当阻抗越小时，由于 U 2 = I2 Z，会
－ I0 N1
ε = I N
I0
× 100% = I'
= － Z'02
Z
× 100% = － Z02
Z'
使得输出电压值变小。最终通过实验得到阻抗为 100
Ω 时，测量结果最理想。
1 1 2 m
m
( 4)
2 信号调理及误差测量
式中: Z02 为二次侧的总阻抗; Zm 为励磁电阻。
通过运算后发现，误差与二次侧的总阻抗和励磁
阻抗有关。由于励磁电阻是非线性的，被测电流变化时，磁通密度的不同，会导致励磁电阻发生变化。因此将误差转换成线性物理量进行研究。
由图 2 可以得出:
－ E
1. 1 信号调理电路
考虑到传感器产生的电压信号在 μV 级，容易受噪声的影响。需利用信号调理电路对微弱信号进行放大滤波等处理［6］。整个信号处理部分的噪声情况主要是由第一级的放大电路来决定。在设计微弱信号检测电路时，必须确保第一级噪声足够小。选择仪
表放大器 AD620AN 组建前置放大电路［7］。仪表放大
I0
= 1
Zm
( 5)
器用差分放大，对共模噪声具有很强的抑制作用，适
又根据电磁感应定律求得磁密 B m 与 E 2 的关系:
合用来对微弱信号进行前置放大。
B m
jE × 108
= 2
4. 44fN2 SK
( 6)
为获得稳定的数据，应对放大后的信号进行有源
滤波，平滑地滤去不需要的干扰。由于电压信号为正
磁场强度与磁感应强度的关系为
μ～ = Bm
误差公式变为
j( Z + Z ) l × 108
ε～ = 2 L
4. 44 2 fN2 μ～ SK
( 7)
( 8)
弦工频信号，因此采用巴特沃兹低通滤波滤除高频干 扰。该滤波电路在通带内的纹波很小，幅频特性平稳，而且在截止频率附近下降速率较快［8］，滤波效率 较高。在实际电路中，对信号进行前置放大和滤波 后，送入中间级和末级放大电路。在对微弱信号进行 检测时，易受来自外界或电流传感器耦合进的噪声，
由式( 8) 可知: 电流传感器的误差与二次回路的
阻抗( Z2 + ZL ) ，铁芯磁路 l，信号频率 f，二次匝数 N2 ，铁芯磁导率 μ～ ，铁芯截面积 S，叠片系数 K 有关。
在电流传感器铁芯材料的选用上，满足测量精度
包括电子器件的噪声，直流偏置及电源纹波的影响。
在通过共模抑制放大电路、模拟滤波、数字滤波等措施减小噪声之外，为进一步避免信号受干扰，分别从以下几个方面抑制噪声:
( 1) 导线连接尽量短，避免信号能量损失。
( 2) 电源使用大容量极性电容并联小电容，滤除电源纹波。
一周期函数 x( t) 可以展开成傅里叶级数:
∞
x( t) = ∑( an cos nωt + bn sin nωt)
n = 0
( 3) 在接地线的处理上，采用并行单点接地。
( 4) 信号处理电路中使用的电阻均为精密电阻。
= A0
∞
+ ∑
n = 1
∞
( an cos nωt + bn
sin nωt)
( 5) 加入 AD620 调零电路。
基于 Multisim 搭建电路模型进行仿真后，搭建了实际的硬件电路。
= A0 + ∑An sin( nωt + φn ) ( 9)
n = 1
式中: a，b 为傅里叶系数; φn 为 n 次谐波的初相位，其
a
2． 2 电流传感器误差的测量
中基波的初相位为 φ1
= 1 。
b
本文设计的是微电流传感器，主要用于测量 mA， μA 级电流，故将额定电流设为 440 μA，根据新修订的测量用互感器检定规程，需对额定电流的 5% ～ 120% 范围内的电流进行比差和角差的测量［9］。关于误差
1
可知只要求出傅里叶级数，就可求出任一谐波的初相位，而相位差测量中只要求出基波的初相位即
可。设周期信号的一个周期内有 N 个采样点。则
N－1
测量，利用虚拟仪器编写程序进行测量。其优点在于: 测量过程抗干扰; 计算速度快; 测量结果精确; 具
a = 2
N k = 0
2 N－1
x( k) cos 2πk
N
2πk
( 10)
有交互性，实时性。基于 LabVIEW 平台，利用数据采集卡 USB － 6009［10］对传感器输出的信号进行采集，存
b1 =
∑x( k) sin
k = 0
a
( 11)
N
储并进行误差分析。
在实际实验中，采集信号易受到电磁干扰、A / D 转换量化误差等因素影响，故在存储数据前，为保证
φ = arctan 1
b1
因此两路信号基波分量的相位差:
φ = arctan a11 － arctan a21
( 12)
( 13)
运算结果的精确性，需利用 LabVIEW 中的滤波器将
DAQ 采集到的数据进行数字滤波。针对信号微弱易
3 实验及结果分析
b11
b21
受纹波影响的情况，采用 IIＲ 型巴特沃斯滤波器［11］。误差测量主要包括比差和角差的测量。根据式
( 2) ，需要得到一次侧电流和二次侧电流幅值，将二次侧电流幅值乘以变比 K1n 与一次侧电流幅值进行比较。通过 LabVIEW 中的峰值检测 VI 获取波形幅值。
角差是二次电流反向后，与一次电流相角之差。由于 传感器输出的电压信号微弱，要求角差测量的结果精 度高，抗干扰性强。通过分别编写过零检测法，相关 法与频谱分析法 3 种相位差测量程序，在采样率为10 kHz，信号频率为 50 Hz，幅值为 5 V，相位差为 1°，加入噪声后的情况下比较测量结果。如表 1 所示。
表 1 相位误差测量结果
测量方法 真实相位/( °) 采样频率/ kHz 测得相位差/( °) 误差/%
|
过零检测法 |
30 |
10 |
26． 651 3 |
－ 1． 162 3 |
|
相关法 |
30 |
10 |
30． 295 3 |
0． 984 3 |
|
频谱分析法 |
30 |
10 |
30． 005 2 |
0． 017 3 |
从表 1 可知，频谱分析法更稳定，测量结果更准确。因此采用频谱分析法进行相位误差的测量，该方法可以避免谐波的影响［12］，对噪声和干扰有一定的抑制作用，测量精度高。利用虚拟仪器频谱分析法测量误差的原理为: 在有效区间( t，t + T) 内，绝对可积的任
在实验条件下，利用信号发生器发出电压信号，
加在取样电阻两端。根据图3 加入信号处理模块进行实验，观察信号输出波形。
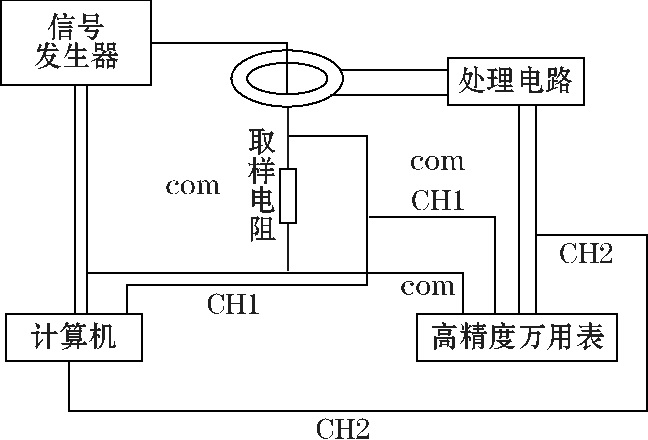
图 3 实验测量图
图 4 为电流传感器输出电压为 30 μV 时，信号处理电路输出的电压波形图。
由图 4 可知，微弱信号经过放大滤波后输出的信号幅值为 0． 25 V，其中信号处理电路的总增益为 8 533。该电路可以精确地放大 μV 级电压信号，适合用于放大传感器微弱信号。提高了测量的稳定性，便于进行误差测量。
对输出信号进行 FFT 分析，由图 5、图 6 可知通过滤波电路以及利用多种抗干扰措施后，高频噪声幅度
表 3 比差测量结果
|
电流值 / μA |
电流百 分比/% |
幅值误 差值/% |
电流值 / μA |
电流百 分比/% |
幅值误 差值/% |
|
22 |
5 |
－ 0． 52 |
264 |
60 |
－ 0． 75 |
|
44 |
10 |
－ 0． 43 |
352 |
80 |
－ 1． 08 |
|
88 |
20 |
－ 0． 78 |
440 |
100 |
－ 1． 61 |
|
176 |
40 |
－ 1． 23 |
528 |
120 |
－ 0． 75 |
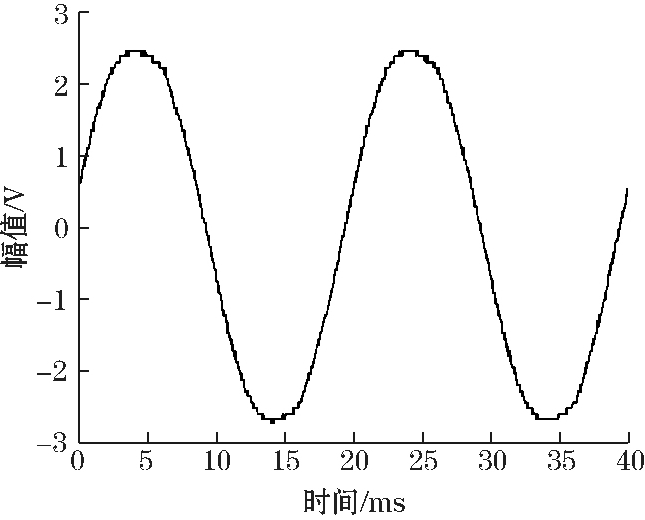
图 4 输出信号波形图
衰减了 32 dB，基本被滤除，提高了测量系统的信噪比，保证了输出数据的稳定性。
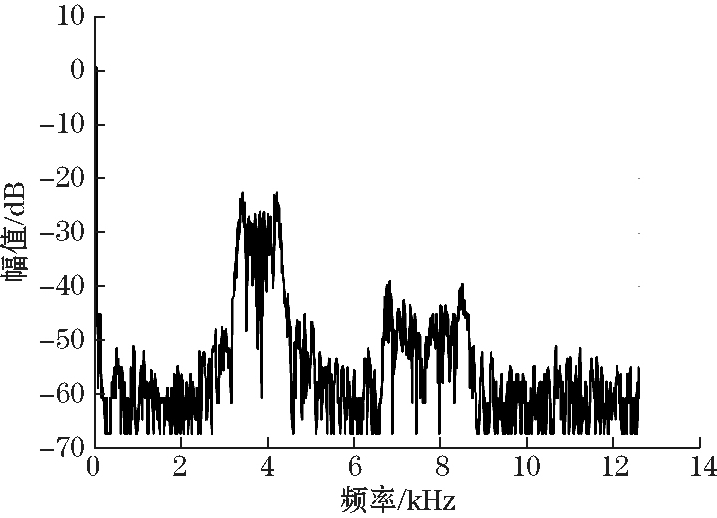
图 5 对信号进行处理前的 FFT 图
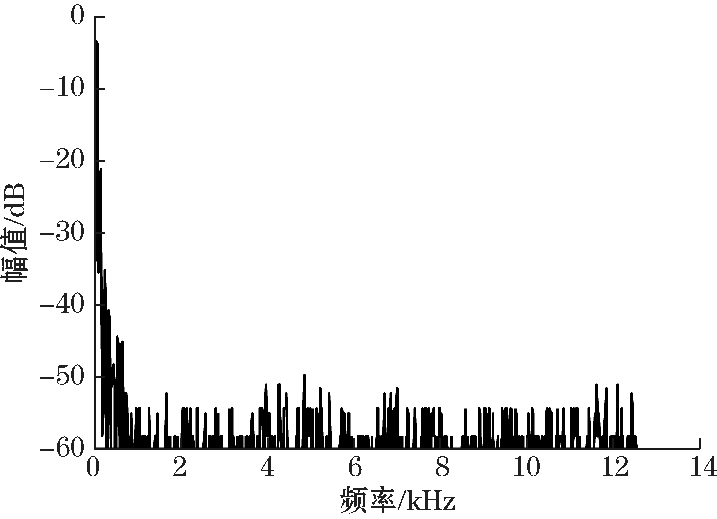
图 6 对信号进行处理后的 FFT 图
在实验室环境下，利用信号发生器发出信号与电流传感器感应到的信号经过信号处理后，分别通过采集卡送入 LabVIEW 进行存储。对两路信号进行误差的比较。测量结果如表 2、表 3 所示。
表 2 角差测量结果
搭建的软件滤波电路滤波效果好，总谐波失真度为 4． 2% ，输出波形特性良好。搭建的误差测量程序运行正常，可以准确地测量比差和角差，并显示原边和副边的波形，使得整个测量系统更精确，更具交互性。
从表 2、表 3 测量结果可知，该微电流传感器的测量范围在 20 ～ 500 μA。当原边电流为额定电流，误差最小。根据《测量用互感器检定规程》中关于电流传感器误差的规定，电流传感器的比差达到了 0． 5 级的准确度。
3 结束语
针对普通小电流传感器难以测量 μA 级泄漏电流的问题。通过分析电磁式电流传感器的误差影响因素， 设计了一种高精度的微电流传感器。研究成果如下:
( 1) 研制了测量下限为 20 μA 的微电流传感器。根据测量用互感器检定规程，电流传感器比差的准确度达到 0． 5 级。
( 2) 设计了微弱信号调理电路，30 μV 电压信号经由总增益为8 533 的放大滤波电路后输出 0． 256 V电压，该电路可以准确放大微弱信号。经 FFT 分析得高频噪声衰减了 32 dB，提高了信噪比，增强了整个系统的抗干扰性。
( 3) 基于 LabVIEW 平台利用频谱分析法编写了测量比差和角差的程序，该方法精度为0． 017 3% ，提高了误差测量结果的精确性和稳定性，使测量结果更具可视化，交互性。
参考文献:
［1］ 包军，田建华，张秀阁． 基于零磁通原理的高精度小电流传感器的研究［J］． 电力系统保护与控制，2002，30( 12) : 32 － 33．
［2］ 赵修民． 测量用互感器［M］． 北京: 机械工业出版社，
1984: 50 － 52; 62 － 63．
［3］ 李培艳． 基于零磁通的无源单匝穿心式小电流互感器的研究［D］． 哈尔滨: 哈尔滨工业大学，2006．
［4］ ＲISTESKA A，CHAN K Y，GOＲDIJN A，et al． Electrical sta- bility of high-mobility microcrystalline silicon thin-film tran- sistors［J］． Journal of Display Technology，2012，8 ( 1 ) : 27
－ 34．